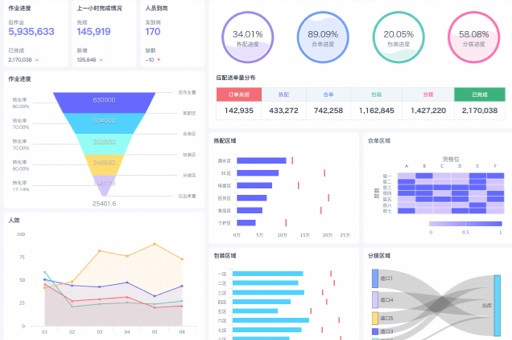
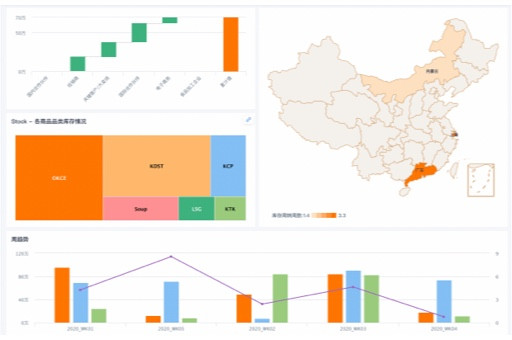
一、实时OLAP的查询响应速度陷阱

在OLAP（联机分析处理）领域，实时OLAP的查询响应速度常常被视为关键指标。许多企业在选择OLAP工具时，会将快速的查询响应速度作为首要考虑因素。然而，这里存在一个常见的陷阱。

从数据仓库的角度来看，数据的处理和存储方式会对查询响应速度产生重大影响。ETL（抽取、转换、加载）过程如果不够高效，会导致数据延迟进入数据仓库，进而影响实时OLAP的查询结果。例如，一些初创企业在搭建数据仓库初期，由于技术团队经验不足，ETL流程设计不合理，可能会出现数据抽取不及时、转换规则错误等问题，使得实时OLAP查询时无法获取最新、最准确的数据。

在电商场景下，实时OLAP的应用尤为重要。比如一家独角兽电商企业，希望通过实时OLAP分析用户的购买行为，以便及时调整营销策略。但如果查询响应速度过快，可能会导致数据不准确。行业平均的实时OLAP查询响应速度在500毫秒到1秒之间，有些企业为了追求极致的速度，可能会简化数据处理流程，忽略数据的完整性和准确性。这样一来，虽然查询速度上去了，但基于这些不准确数据做出的商业智能决策可能会给企业带来巨大损失。

误区警示：不要盲目追求实时OLAP的查询响应速度，而忽略了数据的质量和完整性。在选择OLAP工具时，要综合考虑工具的数据处理能力、ETL效率以及对数据准确性的保障。

二、星型模型与雪花模型的存储效率公式

在数据建模中，星型模型和雪花模型是两种常见的模型。它们在存储效率上有着不同的特点，我们可以通过一些公式来进行分析。

星型模型的存储效率主要与事实表和维度表的大小有关。假设事实表的记录数为F，维度表的平均记录数为D，维度表的数量为n。那么星型模型的存储空间S_star可以表示为：S_star = F + n * D。

雪花模型则是对星型模型的进一步规范化，它将维度表进行了细分。假设雪花模型中细分后的维度表数量为m，每个细分维度表的平均记录数为d。那么雪花模型的存储空间S_snowflake可以表示为：S_snowflake = F + m * d。

以一家上市电商企业为例，其事实表记录了每天的订单信息，记录数大约为100万条。维度表包括用户维度、商品维度、时间维度等，平均每个维度表有10万条记录，维度表数量为5个。那么按照星型模型计算，存储空间大约为100万 + 5 * 10万 = 150万条记录的空间。

如果采用雪花模型，将用户维度进一步细分为用户基本信息维度、用户行为维度等，细分后的维度表数量增加到8个，每个细分维度表平均有5万条记录。那么雪花模型的存储空间大约为100万 + 8 * 5万 = 140万条记录的空间。

成本计算器：通过上述公式，企业可以根据自身的数据量和业务需求，计算出使用星型模型和雪花模型的存储成本，从而选择更适合自己的模型。

三、内存计算技术的ROI临界点

内存计算技术在OLAP中扮演着重要角色，它可以显著提高查询性能。然而，企业在采用内存计算技术时，需要考虑其ROI（投资回报率）临界点。

从商业智能决策的角度来看，采用内存计算技术可以快速获取数据分析结果，帮助企业及时做出决策，从而带来更多的商业价值。但同时，内存计算技术需要投入大量的硬件成本和维护成本。

以一家位于技术热点地区的初创企业为例，该企业计划采用内存计算技术来提升OLAP的性能。假设企业每年的业务增长带来的额外收益为R，采用内存计算技术的硬件成本为C_hardware，维护成本为C_maintenance，使用年限为n年。那么ROI可以表示为：ROI = (R * n - C_hardware - C_maintenance) / (C_hardware + C_maintenance)。

行业平均的内存计算技术ROI临界点在20%到30%之间。如果企业的ROI低于这个临界点，那么采用内存计算技术可能并不划算。例如，该初创企业采用内存计算技术的硬件成本为50万元，维护成本每年为10万元，使用年限为3年。每年业务增长带来的额外收益为30万元。那么ROI = (30 * 3 - 50 - 10 * 3) / (50 + 10 * 3) = 10 / 80 = 12.5%，低于行业平均的ROI临界点。

技术原理卡：内存计算技术是将数据存储在内存中进行计算，避免了频繁的磁盘I/O操作，从而提高了计算速度。但由于内存的成本较高，企业需要谨慎评估其ROI。

四、增量更新的数据新鲜度悖论

在数据仓库中，增量更新是一种常用的数据更新方式，它可以保证数据的新鲜度。然而，这里存在一个悖论。

从ETL的角度来看，增量更新可以减少数据处理的时间和资源消耗。例如，一家独角兽电商企业每天会产生大量的订单数据，如果采用全量更新，每次都需要处理所有的订单数据，这会耗费大量的时间和计算资源。而采用增量更新，只需要处理当天新增的订单数据，大大提高了ETL的效率。

但在实际应用中，增量更新可能会导致数据新鲜度的问题。假设增量更新的时间间隔为T，在T时间内，数据仓库中的数据可能已经过时。例如，电商企业的促销活动可能会在短时间内产生大量的订单，如果增量更新的时间间隔为1小时，那么在这1小时内，数据仓库中的数据就无法及时反映促销活动的效果。

行业平均的增量更新时间间隔在15分钟到30分钟之间。一些企业为了追求数据的新鲜度，可能会缩短增量更新的时间间隔，但这会增加ETL的负担和成本。

误区警示：企业在采用增量更新时，要综合考虑数据的重要性、业务需求以及ETL的成本和效率，找到一个合适的增量更新时间间隔，避免陷入数据新鲜度悖论。

五、反直觉：全量预计算的经济学模型

在OLAP中，全量预计算是一种常见的优化方式。然而，它的经济学模型可能与我们的直觉不同。

从商业智能决策的角度来看，全量预计算可以提前计算出所有可能的查询结果，从而提高查询性能。但这需要投入大量的计算资源和存储空间。

以一家上市电商企业为例，该企业有大量的历史订单数据和用户行为数据。如果采用全量预计算，需要对这些数据进行全面的计算和存储。假设全量预计算的计算成本为C_compute，存储成本为C_storage，查询性能提升带来的收益为R。那么全量预计算的经济学模型可以表示为：收益 = R - C_compute - C_storage。

行业平均的全量预计算成本占企业IT总预算的10%到20%。一些企业可能会认为全量预计算可以一劳永逸地解决查询性能问题，但实际上，随着数据量的不断增长，全量预计算的成本也会不断增加。

成本计算器：企业可以根据自身的数据量、查询需求以及IT预算，计算出全量预计算的成本和收益，从而判断是否采用全量预计算。

本文编辑：帆帆，来自Jiasou TideFlow AI SEO 创作