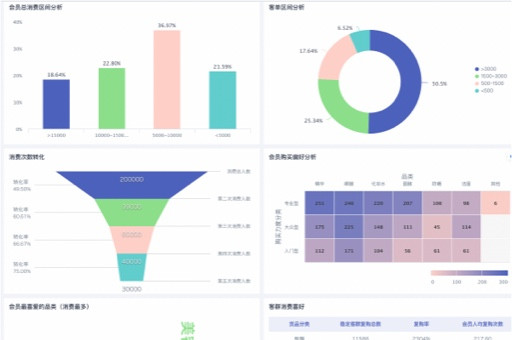
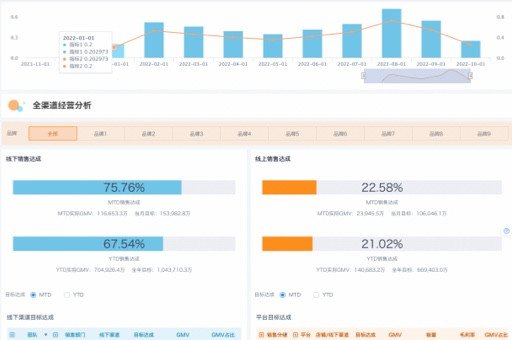
鸢尾花数据集是机器学习领域中最著名的数据集之一，被广泛用于分类算法和数据可视化的研究。它包含了150个样本，每个样本都有四个特征：花萼长度、花萼宽度、花瓣长度和花瓣宽度。这些特征用于区分三个不同种类的鸢尾花：山鸢尾（Setosa）、变色鸢尾（Versicolor）和维吉尼亚鸢尾（Virginica）。

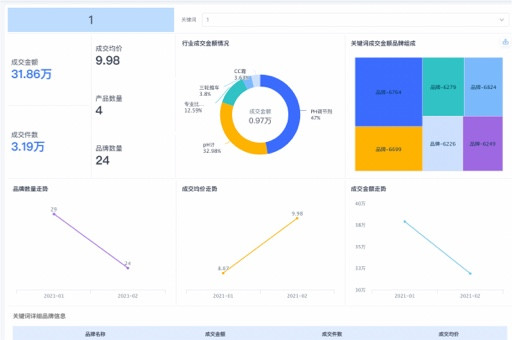
为了更好地理解鸢尾花数据集，我们可以通过可视化方法来探索数据中的隐藏信息。通过使用Python的数据分析和可视化库，如NumPy、pandas和matplotlib，我们可以将数据可视化成散点图、箱线图和直方图，以便更好地观察和理解数据的分布情况。

散点图：探索特征之间的关系

散点图是一种用于观察两个特征之间关系的常用图表。在鸢尾花数据集中，我们可以使用散点图来探索花萼长度和花萼宽度之间的关系，或者花瓣长度和花瓣宽度之间的关系。通过观察散点图的分布，我们可以判断特征之间是否存在相关性。

例如，我们可以绘制花萼长度和花萼宽度的散点图，用不同颜色来表示不同种类的鸢尾花。如果我们发现不同鸢尾花种类在散点图中呈现出明显的区分，那么我们可以初步判断花萼长度和花萼宽度可能是区分鸢尾花种类的重要特征。

箱线图：观察特征的分布情况

箱线图是一种常用的统计图表，用于显示一组数据的分布情况。在鸢尾花数据集中，我们可以使用箱线图来观察花瓣长度在不同种类的鸢尾花中的分布情况。

通过绘制不同鸢尾花种类的花瓣长度的箱线图，我们可以直观地观察到它们的中位数、上下四分位数和异常值。这有助于我们理解不同鸢尾花种类的花瓣长度的分布范围和差异。

直方图：了解特征的频数分布

直方图是一种常用的图表，用于显示连续变量的频数分布情况。在鸢尾花数据集中，我们可以使用直方图来观察花瓣宽度的频数分布情况。

通过绘制花瓣宽度的直方图，我们可以观察到不同花瓣宽度范围内样本的数量，并且可以判断花瓣宽度是否呈现正态分布。这有助于我们进一步理解花瓣宽度这一特征在鸢尾花数据集中的分布情况。

通过以上的可视化方法，我们可以更加深入地了解鸢尾花数据集，从而为后续的分类算法和模型构建提供更准确的特征选择和数据分析基础。